Poker 2 Pair High Card
- High Card is the worst possible hand on the poker hand rankings list. It consists of no pair or any other hand type – just a high card. The words “High Card” should have you thinking straight away about a hand with the highest card.
- The One Pair is ranked based on the denomination of the two matching cards, with Ace being the highest one and 2 being the lowest. For example, a J-J-4-3-2 hand is stronger than 10-10-A-J-7.
The biggest adjustment when playing heads-up poker is that marginal hands go way up in value. 3rd pair or even high card Ace can often win at showdown. So, loosen up and don’t let your opponent run you over if he or she bets a lot! Two pairs a pair high card The total number of 7-card poker hands is. We shall count straight flushes using the largest card in the straight flush. This enables us to pick up 6- and 7-card straight flushes. When the largest card in the straight flush is an ace, then the 2 other cards may be any 2 of the 47 remaining cards.
Brian Alspach
17 January 2000
Abstract:
There are a few 6-card poker games so it is worth looking at probabilitiesfor winning with certain kinds of hands. One chooses the highest ranked5-card poker hand among the 6 cards and values the hand based on the5-card hand. The types of 5-card poker hands in decreasing rank are
- straight flush
- 4-of-a-kind
- full house
- flush
- straight
- 3-of-a-kind
- two pairs
- a pair
- high card
The total number of 6-card poker hands is .
A straight flush is completely determined once the smallest card in thestraight flush is known. There are 40 cards eligible to be the smallestcard in a straight flush. If the smallest card in the straight flush isan ace, then the sixth card may be any of 47 cards. If the smallest cardin the straight flush is any of the other 36 eligible beginning cards,then the sixth card may be any of 46 cards because we cannot use the nextsmallest card in the same suit as the straight flush. Hence, there are6-card hands containing straight flushes.
In forming a 4-of-a-kind hand, there are 13 choices for the rank ofthe quads, 1 choice for the 4 cards of the given rank, and choices for the remaining 2 cards. This implies there are 4-of-a-kind hands.
Two Pair Poker Hand
There are 2 ways to get a full house and we count them separately. Oneway of obtaining a full house is for the 6-card hand to contain 2 setsof triples. There are ways to choose the 2 ranksand 4 ways to choose each of the triples. This gives us full houses of this type. The other way of getting a full houseis for the 6-card hand to contain a triple, a pair and a remaining card ofa third rank. There are 13 choices for the rank of the triple, 12 choicesfor the rank of the pair, and 44 choices for the singleton card. Thereare 4 ways of choosing the triple of a given rank and 6 ways to choose thepair of the other rank. This produces full houses of the latter type. Adding the two numbersyields 165,984 full houses.
To count the number of flushes, we obtain 6-card hands formed from cards in the same suit. Altogether, thereare flushes with 6 cards in the same suit.There are choices for 5 cards in the same suit.There are then 39 choices for a sixth card from a different suit. Thus,there are flushes in 6-card hands, whereprecisely 5 cards are in the same suit. Combining the two gives us207,636 6-card hands containing flushes. Of these, 1,844 are straightflushes whose removal leaves 205,792 flushes.
Let's determine how many sets of 6 distinct ranks correspond to straights.One possible form is ,where x can be any of9 ranks. The other possible form is ,where yis neither x-1 nor x+5. When x is ace or 10, then there are 7choices for y. When x is between 2 and 9, inclusive, there are 6choices for y. This implies there are sets of 6 distinct ranks corresponding to straights. There are then 4choices for each card of the given ranks except we must remove thosechoices producing flushes. There are 4 choices giving all 6 cards inthe same suit. If 5 are in the same suit, there are choices of which 5 ranks will be in the same suit, 4 choicesfor the suit of the 5 cards, and 3 choices for the suit of the remainingcard. So there are choices which give aflush. This means there are 46 - 76 = 4,020 choices not producing aflush. Hence, there are straights of thisform.
We also can have a set of 5 distinct ranks producing a straight whichmeans the corresponding 6-card hand must contain a pair as well. Thereare 10 sets of ranks of the form .There are 5choices of the rank to be paired, 6 choices for the pair, and 4 choicesfor each of the other 4 cards except not all 4 cards can be chosen inthe same suit as either of the cards in the pair. This means there are44 - 2 = 254 choices for the 4 cards. We then have straights of this form. Altogether there are361,620 straights.
In forming a 3-of-a-kind hand, there must be a triple and 3 other cardsall of distinct ranks different from the rank of the triple. There are13 choices for the rank of the triple, and there are choices for the ranks of the other 3 cards. There are 4 choicesfor the triple of the given rank and there are 4 choices for each of thecards of the remaining 3 ranks. Altogether, we have 3-of-a-kind hands.
Next we consider two pairs hands. Such a hand may contain either threepairs, or two pairs plus two remaining cards of distinct ranks. Weevaluate these 2 types of hands separately. If the hand has threepairs, there are ways to choose the ranks ofthe pairs and 6 ways to choose each of the pairs. This produces6-card hands with three pairs.
For the other kind of two pairs hand, there are choices for the two ranks of the pairs and there are ways to choose the ranks of the 2 singletons. There are 6 choicesfor each of the pairs, and there are 4 choices for each of the remaining2 cards. This produces hands of two pairs of the second type. Adding the two gives 2,532,8166-card hands with two pairs.
Now we count the number of hands with a pair. Such a hand must have5 distinct ranks. There are possible setsof 5 ranks. We must remove sets of the form because these correspond to straights. There are 10 such sets leaving1,277 sets of ranks corresponding to a hand with one pair. Given sucha set, there are 5 choices for the rank of the pair, and 6 choices fora pair of the chosen rank. There are 4 choices for each of the remaining4 cards except we cannot choose all 4 to be in the same suit as eitherof the cards forming the pair. Hence, there are 44-2 = 254 choicesfor the remaining 4 cards. This gives us hands with a pair.
We could determine the number of high card hands by removing the handswhich have already been counted in one of the previous categories.Instead, let us count them independently and see if the numbers sumto 20,358,520 which will serve as a check on our arithmetic.
A high card hand has 6 distinct ranks, but does not include straights.So we must eliminate sets of ranks which have 5 consecutive ranks. Indetermining the number of straights above, we derived that there are 71sets of 6 distinct ranks which give straights. There are sets of 6 distinct ranks. Removing the 71 sets correspondingto straights, leaves 1,645 sets of distinct ranks which do not producestraights. There are 4 choices for each of the 6 cards in a given setproducing 46 = 4,096 ways of choosing cards for a given set of ranks.However, some of the choices produce flushes and we must remove them.Clearly there are 4 ways of choosing the 6 cards all in the same suitwhich is one way of getting a flush. There 6 ways of choosing 5 of theranks and 4 choices for the suit of these 5 ranks, and 3 choices for thesuit of the remaining card. This gives us choices of suits which produce a flush with 5 cards in the same suit.We remove these 76 choices which produce flushes giving us 4,020 choicesfor the 6 cards which do not produce a flush. Multiplying 4,020 by 1,645gives 6,612,900 high card hands.
If we sum the preceding numbers, we obtain 20,358,520 and we can be confidentthe numbers are correct.
Here is a table summarizing the number of 6-card poker hands. Theprobability is the probability of having the hand dealt to you whendealt 6 cards.
| hand | number | Probability |
| straight flush | 1,844 | .000091 |
| 4-of-a-kind | 14,664 | .00072 |
| full house | 165,984 | .00815 |
| flush | 205,792 | .0101 |
| straight | 361,620 | .0178 |
| 3-of-a-kind | 732,160 | .036 |
| two pairs | 2,532,816 | .1244 |
| pair | 9,730,740 | .478 |
| high card | 6,612,900 | .325 |
You will observe that you are less likely to be dealt a hand withno pair (or better) than to be dealt a hand with one pair. Thishas caused some people to query the ranking of these two hands.In fact, if you were ranking 6-card hands based on 6 cards, theorder of the last 2 would switch. However, you are basing the rankingon 5 cards so that if you were to rank a high card hand higher than a handwith a single pair, people would choose to ignore the pair in a6-card hand with a single pair and call it a high card hand. Thiswould have the effect of creating the following distortion. Thereare 16,343,640 6-card hands containing 5 cards which are high cardhands. Of these 16,343,640 hands, 9,730,740 also contain 5-cardhands which have a pair. Thus, the latter hands are more specialand should be ranked higher (as they indeed are) but would not beunder the scheme being discussed in this paragraph.
last updated 12 January 2000
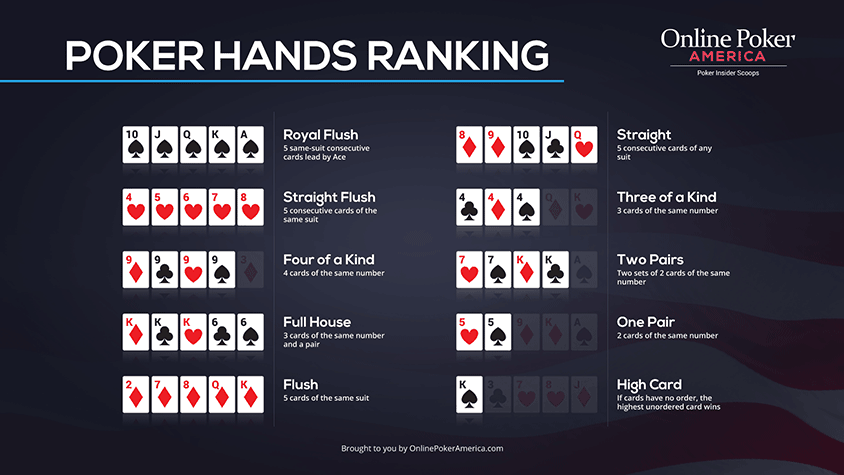
Below is the complete guide for determining how to rank various poker hands. This article covers all poker hands, from hands in standard games of poker, to lowball, to playing with a variety of wild cards. Scroll to the end to find an in-depth ranking of suits for several countries, including many European countries and North American continental standards.
Standard Poker Rankings
A standard deck of cards has 52 in a pack. Individually cards rank, high to low:
Ace, King, Queen, Jack, 10, 9, 8, 7, 6, 5, 4, 3, 2
In standard poker (in North America) there is no suit ranking. A poker hand has 5 cards total. Higher ranked hands beat lower ones, and within the same kind of hand higher value cards beat lower value cards.
#1 Straight Flush
In games without wild cards, this is the highest ranking hand. It consists of five cards in sequence of the same suit. When comparing flushes, the hand with the highest value high card wins. Example: 5-6-7-8-9, all spades, is a straight flush. A-K-Q-J-10 is the highest ranking straight flush and is called a Royal Flush. Flushes are not permitted to turn the corner, for example, 3-2-A-K-Q is not a straight flush.
#2 Four of a Kind (Quads)
A four of a kind is four cards of equal rank, for example, four jacks. The kicker, the fifth card, may be any other card. When comparing two four of a kinds, the highest value set wins. For example, 5-5-5-5-J is beat by 10-10-10-10-2. If two players happen to have a four of a kind of equal value, the player with the highest ranking kicker wins.
#3 Full House (Boat)
A full house consists of 3 cards of one rank and 2 cards of another. The three cards value determines rank within Full Houses, the player with the highest rank 3 cards wins. If the three cards are equal rank the pairs decide. Example: Q-Q-Q-3-3 beats 10-10-10-A-A BUT 10-10-10-A-A would beat 10-10-10-J-J.
#4 Flush
Any five cards of the same suit. The highest card in a flush determines its rank between other flushes. If those are equal, continue comparing the next highest cards until a winner can be determined.
#5 Straight
Five cards in sequence from different suits. The hand with the highest ranking top card wins within straights. Ace can either be a high card or low card, but not both. The wheel, or the lowest straight, is 5-4-3-2-A, where the top card is five.
#6 Three of a Kind (Triplets/Trips)
A three of a kind is three card of equal rank and two other cards (not of equal rank). The three of a kind with the highest rank wins, in the event they are equal, the high card of the two remaining cards determines the winner.
#7 Two Pairs
A pair is two cards that are equal in rank. A hand with two pairs consists of two separate pairs of different ranks. For example, K-K-3-3-6, where 6 is the odd card. The hand with the highest pair wins if there are multiple two pairs regardless of the other cards in hand. To demonstrate, K-K-5-5-2 beats Q-Q-10-10-9 because K > Q, despite 10 > 5.
#8 Pair
A hand with a single pair has two cards of equal rank and three other cards of any rank (as long as none are the same.) When comparing pairs, the one with highest value cards wins. If they are equal, compare the highest value oddball cards, if those are equal continue comparing until a win can be determined. An example hand would be: 10-10-6-3-2
#9 High Card (Nothing/No Pair)
If your hand does not conform to any of the criterion mentioned above, does not form any sort of sequence, and are at least two different suits, this hand is called high card. The highest value card, when comparing these hands, determines the winning hand.
Low Poker Hand Ranking
In Lowball or high-low games, or other poker games which lowest ranking hand wins, they are ranked accordingly.
A low hand with no combination is named by it’s highest ranking card. For example, a hand with 10-6-5-3-2 is described as “10-down” or “10-low.”
Ace to Five
The most common system for ranking low hands. Aces are always low card and straights and flushes do not count. Under Ace-to-5, 5-4-3-2-A is the best hand. As with standard poker, hands compared by the high card. So, 6-4-3-2-A beats 6-5-3-2-A AND beats 7-4-3-2-A. This is because 4 < 5 and 6 < 7.
The best hand with a pair is A-A-4-3-2, this is often referred to as California Lowball. In high-low games of poker, there is often a conditioned employed called “eight or better” which qualifies players to win part of the pot. Their hand must have an 8 or lower to be considered. The worst hand under this condition would be 8-7-6-5-4.
Duece to Seven
The hands under this system rank almost the same as in standard poker. It includes straights and flushes, lowest hand wins. However, this system always considers aces as high cards (A-2-3-4-5 is not a straight.) Under this system, the best hand is 7-5-4-3-2 (in mixed suits), a reference to its namesake. As always, highest card is compared first. In duece-to-7, the best hand with a pair is 2-2-5-4-3, although is beat by A-K-Q-J-9, the worst hand with high cards. This is sometimes referred to as “Kansas City Lowball.”
Ace to Six
This is the system often used in home poker games, straights and flushes count, and aces are low cards. Under Ace-to-6, 5-4-3-2-A is a bad hand because it is a straight. The best low hand is 6-4-3-2-A. Since aces are low, A-K-Q-J-10 is not a straight and is considered king-down (or king-low). Ace is low card so K-Q-J-10-A is lower than K-Q-J-10-2. A pair of aces also beats a pair of twos.
In games with more than five cards, players can choose to not use their highest value cards in order to assemble the lowest hand possible.
Hand Rankings with Wild Cards
Wild cards may be used to substitute any card a player may need to make a particular hand. Jokers are often used as wild cards and are added to the deck (making the game played with 54 as opposed to 52 cards). If players choose to stick with a standard deck, 1+ cards may be determined at the start as wild cards. For example, all the twos in the deck (deuces wild) or the “one-eyed jacks” (the jacks of hearts and spades).
Wild cards can be used to:
- substitute any card not in a player’s hand OR
- make a special “five of a kind”
Five of a Kind
Two Pairs In Poker
Five of a Kind is the highest hand of all and beats a Royal Flush. When comparing five of a kinds, the highest value five cards win. Aces are the highest card of all.
The Bug
Some poker games, most notably five card draw, are played with the bug. The bug is an added joker which functions as a limited wild card. It may only be used as an ace or a card needed to complete a straight or a flush. Under this system, the highest hand is a five of a kind of aces, but no other five of a kind is legal. In a hand, with any other four of a kind the joker counts as an ace kicker.
Wild Cards – Low Poker
During a low poker game, the wild card is a “fitter,” a card used to complete a hand which is of lowest value in the low hand ranking system used. In standard poker, 6-5-3-2-joker would be considered 6-6-5-3-2. In ace-to-five, the wild card would be an ace, and deuce-to-seven the wild card would be a 7.
Lowest Card Wild
Home poker games may play with player’s lowest, or lowest concealed card, as a wild card. This applies to the card of lowest value during the showdown. Aces are considered high and two low under this variant.

Double Ace Flush
This variant allows the wild card to be ANY card, including one already held by a player. This allows for the opportunity to have a double ace flush.
Natural Hand v. Wild Hand
There is a house rule which says a “natural hand” beats a hand that is equal to it with wild cards. Hands with more wild cards may be considered “more wild” and therefore beat by a less wild hand with only one wild card. This rule must be agreed upon before the deal begins.
Incomplete Hands
If you are comparing hands in a variant of poker which there are less than five cards, there are no straights, flushes, or full houses. There is only four of a kind, three of a kind, pairs (2 pairs and single pairs), and high card. If the hand has an even number of cards there may not be a kicker.
Examples of scoring incomplete hands:
10-10-K beats 10-10-6-2 because K > 6. However, 10-10-6 is beat by 10-10-6-2 because of the fourth card. Also, a 10 alone will beat 9-6. But, 9-6 beats 9-5-3, and that beats 9-5, which beats 9.
Ranking Suits
In standard poker, suits are NOT ranked. If there are equal hands the pot is split. However, depending on the variant of poker, there are situations when cards must be ranked by suits. For example:
- Drawing cards to pick player’s seats
- Determining the first better in stud poker
- In the event an uneven pot is to be split, determining who gets the odd chip.
Typically in North America (or for English speakers), suits are ranked in reverse alphabetical order.
- Spades (highest suit), Hearts, Diamonds, Clubs (lowest suit)
Suits are ranked differently in other countries/ parts of the world:
- Spades (high suit), Diamonds, Clubs, Hearts (low suit)
- Hearts (high suit), Spades, Diamonds, Clubs (low suit) – Greece and Turkey
- Hearts (high suit), Diamonds, Spades, Clubs (low suit) – Austria and Sweden
- Hearts (high suit), Diamonds, Clubs, Spades (low suit) – Italy
- Diamonds (high suit), Spades, Hearts, Clubs (low suit) – Brazil
- Clubs (high suit), Spades, Hearts, Diamonds (low suit) – Germany
REFERENCES:
http://www.cardplayer.com/rules-of-poker/hand-rankings
2 Card Poker Free
https://www.pagat.com/poker/rules/ranking.html
Poker 2 Pair High Card Games
https://www.partypoker.com/how-to-play/hand-rankings.html