Blackjack Probability
The name blackjack comes from the fact that when blackjack was first introduced in the U.S. It wasn't very popular, so casinos and gambling houses tried offering different bonus payoffs. One of those was a 10-to-1 payoff for a hand consisting of the ace of spades and a black jack (that is, the jack of spades or the jack of clubs). Probability is calculated on the basis of known data but cannot be used to predict exact outcomes, like the outcome of a hand in the game of blackjack, for example. It simply shows you the likelihood of an event happening, based on the knowledge of the number of desired outcomes and the number of all possible outcomes. The probability to get a blackjack (natural): 64 / 1326 =.0483 = 4.83%. 2) Let's do now the calculations for arrangements. (The combinations are also considered boxed arrangements; i.e. The order of the elements does not count). We calculate total arrangements for 52. In this course, you'll analyze three specific casino games: blackjack, craps, and poker. And, while you're learning how to master these games, you'll also strengthen your skills working with many foundational probability topics including probability trees and conditional probability. Blackjack and Probability Chongwu Ruan Math 190S-Hubert Bray July 24, 2017 1 Introduction Blackjack is an usual game in gambling house and to beat the dealer and make money, people have done lots of research on it. They come up with several basic strategy which is consist of three tables corresponding to the different rules.
Blackjack (also known as twenty-one or sometimes pontoon) is one of the most popular casino card games in the world. The name blackjack comes from the fact that when blackjack was first introduced in the U.S. it wasn't very popular, so casinos and gambling houses tried offering different bonus payoffs. One of those was a 10-to-1 payoff for a hand consisting of the ace of spades and a black jack (that is, the jack of spades or the jack of clubs). With the current rules, a blackjack hand doesn't even need to contain a jack.
Blackjack Probability Math
Rules
A blackjack game has a dealer and one or more players. Each player plays against the dealer. All players are initially dealt two cards and the dealer is dealt one card face down and one face up (these are called the hole card and up card respectively). Each player can then hit (ask for an additional card) until her total exceeds 21 (this is called busting) or she decides to stand (stop taking cards for the rest of the hand). Face cards count as 10 and an ace may be counted as 1 or 11. After all of the players have finished, the dealer reveals the hole card and plays the hand with a fixed strategy: hit on 16 or less and stand on 17 or more.
The player loses if she busts and wins if she does not bust and the dealer does (observe that if both the player and the dealer bust, the player loses). Otherwise, the player wins if her total is closer to 21 than the dealer's. If the player wins, she gets twice her bet; if she loses, she loses her money. If the dealer and player tie it is called a 'push;' the player keeps her bet but does not earn any additional money. If the player's first two cards total 21, this is a blackjack and she wins 1.5 times her bet (unless the dealer also has a blackjack, in which case a tie results), so she gets back 2.5 times her bet.
Soft Hand. A hand that contains an ace that can be counted as 11 is called a soft hand, since one cannotbust by taking a card. With soft hands, the basic strategy is to always hit 17 or less and even hit 18 if the dealer's up card is 9 or 10 (where the 10 refers to a 10, J, Q, or K).
Doubling down. After the player is dealt her initial two cards she has the option of doubling her bet and asking for one additional card (which is dealt face down). The player may not hit beyond this single required card. With the basic strategy, you should always double with a total of 11, double with 10 unless the dealer's up card is 10 or A, and double with 9 only against a dealer's 2 to 6. (Some casinos only allow doubling down on 11).
Splitting pairs. At the beginning of a hand, if the player has two cards with the same number (that is, a pair) she has the option of splitting the pair and playing two hands. In principle, a pair of aces should of course be split, but in this case blackjack rules allow you to get only one card on each hand, and getting a 10 does not make a blackjack. With the basic strategy, you should never split 10's, 5's or 4's, always split 8's, and, in the other cases, split against an up card of 2 to 7, but not otherwise.
Strategies for the Player
Blackjack is almost always disadvantageous for the player, meaning that no strategy yields a positive expected payoff for the player. In the long run, whatever you do, you will on average lose money. Exceptions exist: some casinos offer special rules that allow a player using the right strategy to have a positive expected payoff; such casinos are counting on the players making mistakes.
The so called basic strategy is based on the player's point total and the dealer's visible card. It consists of a table that describes what you should do in any situation in the game (you can find an example of this table at Wikipedia). Under the most favorable set of rules, the house advantage against a player using the basic strategy can be as low as 0.16%.
Many people assume that the best strategy for the player is to mimic the dealer. A second conservative strategy is called never bust: hit 11 or less, stand on 12 or more. Each of these strategies leads to a player disadvantage of about 6%.
Edward Thorp, in his 1962 book Beat the Dealer, describes a simple strategy that makes blackjack an almost even game: if the dealer's up card is 2 to 6, play never bust; if it is 7 to ace, mimic the dealer. The exception to this simple rule is that one should hit a 12 if the dealer's up card is 2 or 3. More advanced strategies include features such as taking into account the player's hand composition (as opposed to just considering the point total) and the other players' hands, specially card counting (that consists of keeping track of the cards that have been dealt so as to know the composition of the remaining cards in the deck), and shuffle tracking (which is far more complicated than card counting, and consists in roughly following groups of cards as they are shuffled). These two last strategies are usually forbidden in casinos.What does it mean to have a 0.16% disadvantage?
When discussing casino games, one usually finds statements such as the ones above saying something like: 'the house advantage in this game is about 0.16%'. A first explanation is the following: betting ten dollars each hand, you will in the long run lose an average of 1.6 cents per hand. It would be nice to have an idea of the probability of winning any particular bet when playing some specific strategy. Indeed, we can infer this from the player's disadvantage. Let's take, as an example, the potential 0.16% disadvantage when playing the basic strategy.
Suppose you bet $1 at each of 10,000 bets playing the basic strategy. Let's call p the total probability of winning a pass line bet (so p is the number we are trying to calculate). If p was, for example, 0.5, it would mean that, on average, half the times you should win the bet, so you would win 0.5 · 10,0000 = 5,000 times. Since each time you win a bet you get twice what you bet and each time you lose the bet you lose all the money, you would end up with 5,000 · $2 = $10,000, that is, the same total amountyou bet (10,000 times $1). In this case, the house advantage is 0%, as is the player advantage.
The same idea applies for any p: if you bet 10,000, you should, on average, win the bet 10,000p times, so your average payoff is $20,000p. In our case, the house advantage is 0.16%, so if you play $10,000, on average you end up with $10,000 - $10,000 · 0.0016 = $10,000 - $16 = $9,984. So we only have to solve the equation $20,000p = $9,984 to get p = 0.4992.
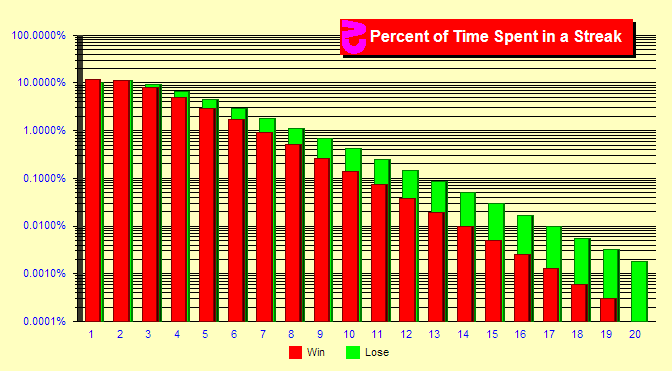
Links
You can find more information on blackjack's rules, strategies, and history on the Internet. For instance, you can try Wikipedia.
A very interesting free on-line blackjack trainer can be found here.
- If you are dealt a point total of 16, what is the probability of busting if you hit, assuming that a whole deck will be used to choose among when you are dealt your next card?
- If you are dealt a 3 and an ace, what is the probability of not busting if you hit, assuming that a whole deck will be used to choose among when you are dealt your next card?
- Suppose you are the only player against the dealer, and you are in the first hand of a game played with one deck. You are dealt an 8 and a 6, while the dealer is showing a queen. What is the probability that you bust if you decide to hit?
| Solutions | Return to Lesson Index | Top of Page |
Bitcoin Chaser - August 28, 2019
Blackjack is one of the most popular gambling card games. It is often hailed for being one of the few games where the player can get an edge over the house. This varies within the different variations and playing rules, but nonetheless, it is still one of more favorable games for the player. To get a picture of the probabilities behind Blackjack, the house edge, and how a player may favor their odds, we take a look at the mathematics of blackjack.
Click here if you are interested to know more about blackjack basics.
Basic Assumptions
To explain blackjack mathematics, we will look at a Blackjack game played with one standard deck.
- This deck pays 1:1 when a player beats the dealer
- 3:2 payed immediately when a player gets Blackjack (21 on the first 2 cards, unless the dealer also gets a Blackjack)
- Returns the bets when there is a “push” or a tie (when the dealer and player have the same numerical value in their hands)
- Dealer stands on 17.
- NOTE: this is the most basic example for illustration purposes and most casinos will have different rules which improve their edge, such as paying 6:5 for Blackjack.
The first and easiest probabilities to look at are those of “busting” after being dealt the first two cards. That is, asking for a third card and going over 21:
| Total Hand Value | Probability of Going Bust |
|---|---|
| 21 | 100% |
| 20 | 92% |
| 19 | 85% |
| 18 | 77% |
| 17 | 69% |
| 16 | 62% |
| 15 | 58% |
| 14 | 56% |
| 13 | 39% |
| 12 | 31% |
| 11 or less | 0% |

Likelihood of Hitting a Blackjack on the First 2 Cards
Here are the possible initial 2-card hands and their probability of being dealt:
| Two Card Combination | Frequency % | Description |
|---|---|---|
| Natural 21 Blackjack | 4.8% | An ace and a 10, J, Q, K |
| Hard Standing (17 – 20) | 30.0% | Two cards that sum 17-20, neither of which is an ace |
| Decision Hands (2-16) | 38.7% | Any hard hand (two non-ace cards) 16 or lower and any soft hand (at least one card is an ace and the other is 9 or lower) |
| No Bust | 26.5% | Any soft hand (Ace plus any card lower than ten) or hard hand (any non-ace cards) summing less than 11. |
| Total (all two card hands) | 100% |
How the House Improves its Edge at Blackjack
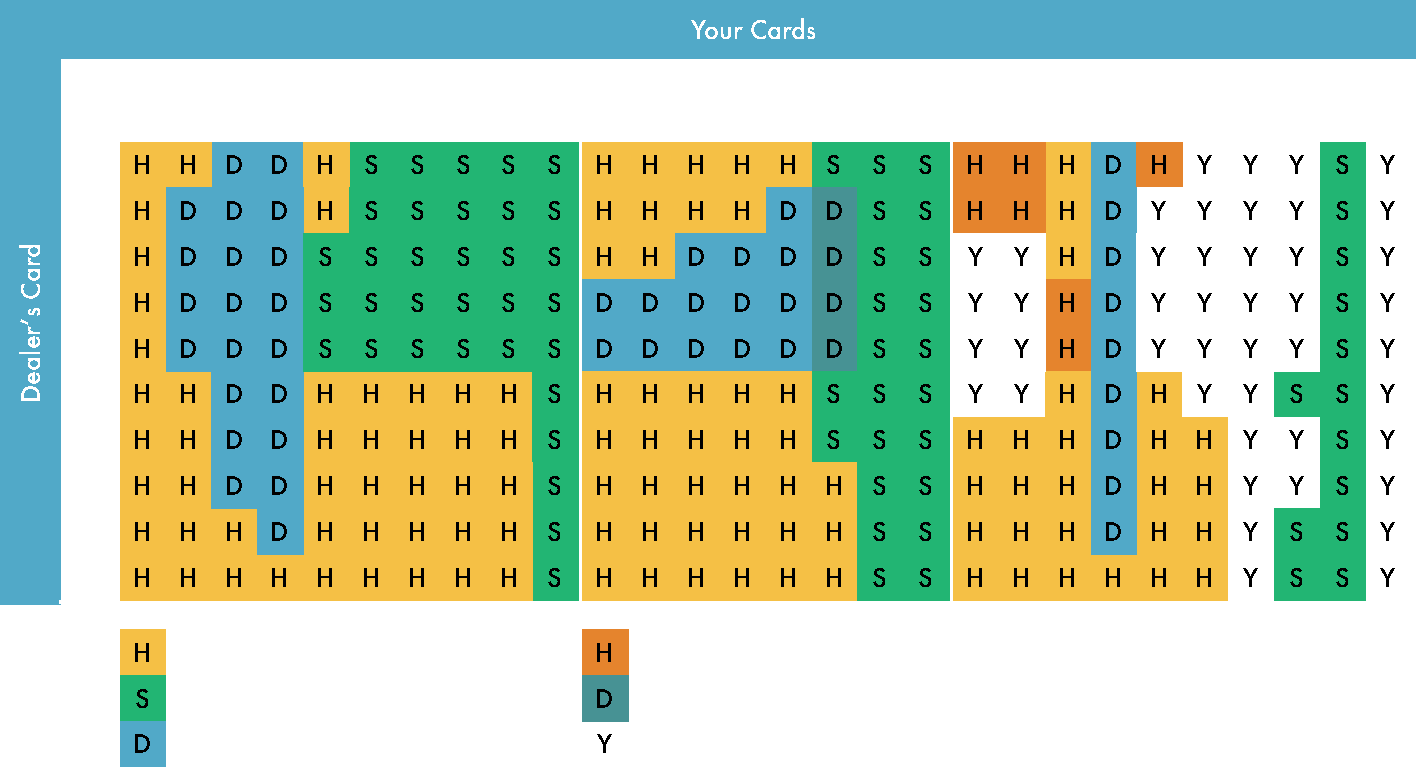
Here is where the house can improve their edge by including more decks. The probability of hitting a Blackjack is reduced from 4.83% to 4.78%. Even though the proportion of cards remains the same when an additional deck is added (4/52 cards are aces in 1 deck = 8/104 cards are aces in 2 decks), the probability of getting a certain hand is not the same (think about removing 1 of four aces in the first deck vs removing 1 out of 8 aces in the case of two decks).
The house can also improve its edge by paying less whenever a player is dealt a Blackjack. While the likelihood of a payout is the same, the payout will be less and the house will increase its edge.
The third basic measure to understand is to look at what the dealer’s final hand will be. Given that the dealer in this case must hit on 16 and stand on 17, the only possible outcomes are that the dealer will have a hand between 17 and 21, or a bust in the following proportions:
| Dealer Final Hand | Probability of Getting Final Hand |
|---|---|
| Natural Blackjack | 4.82% |
| 21 (more than 2 cards) | 7.36% |
| 20 | 17.58% |
| 19 | 13.48% |
| 18 | 13.81% |
| 17 | 14.58% |
| Non-Bust (less than 21) | 71.63% |
| Bust (more than 21) | 28.37% |
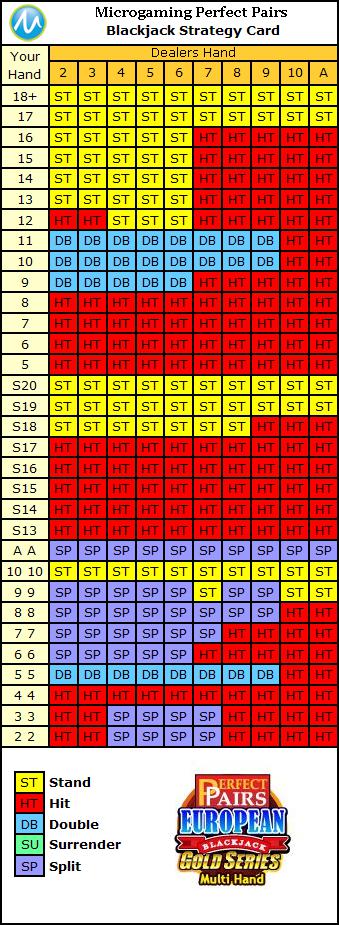
Optimizing your Hand
Given this conclusion, and the knowledge of one of the cards that the dealer holds, a player’s own hand, and the payouts, a strategy can be developed to optimize a player’s earning at blackjack and reduce the house edge from about 8% to below 1%. Such a strategy was developed and is called the basic strategy:
Blackjack Probability Calculation Formula
| Dealer’s Up Card | Dealer’s Odds of Busting | Player Advantage Percentage |
|---|---|---|
| 2 | 35.30% | 9.8% |
| 3 | 37.56% | 13.4% |
| 4 | 40.28% | 18.0% |
| 5 | 42.89% | 23.2% |
| 6 | 42.08% | 23.9% |
| 7 | 25.99% | 14.3% |
| 8 | 23.86% | 5.4% |
| 9 | 23.34% | -4.3% |
| 10 | 21.43% | -16.9% |
| J | 21.43% | -16.9% |
| Q | 21.43% | -16.9% |
| K | 21.43% | -16.9% |
| A | 11.65% | -16.0% |
How does Card Counting Work?
Blackjack Probability Card
There are numerous websites where one can find the basic strategy when playing blackjack under different rules or numbers of decks. However, these do not take into consideration the changing odds after cards are dealt. For that, there is a system of card counting which was developed to increase the probability of winning. This strategy allows a player to gain enough of an edge to beat the house in the long run. But that is a subject for another blog post and is not particularly relevant to online gaming.